بحث عن العبارات الشرطية رياضيات اول ثانوي
تعتبر الرياضيات من الأساسيات التي تقوم عليها العديد من المجالات في حياتنا. هذا العلم العظيم يحتوي على مجموعة واسعة من المفاهيم والمصطلحات الضرورية، التي تلعب دوراً محورياً في فهم واستيعاب الظواهر المختلفة. الرياضيات ليست مجرد أرقام وعمليات حسابية، بل هي لغة عالمية تسهم في تفسير الكون وإيجاد حلول للمشكلات المعقدة. لها تأثيرها الفعّال والبنّاء على مختلف العلوم الأخرى، من الفيزياء إلى البيولوجيا، وتساعد في تقدمها وتطورها. لذا، نركز في دراستنا على التعمق في فهم العبارات الشرطية، وهي مفهوم رياضياتي يسهم في بناء الأسس لفهم أعمق لموضوعات أكثر تعقيداً في هذا العلم الشاسع.
ما هي العبارات الشرطية
تلعب الجمل الشرطية دورًا هامًا في صياغة الأفكار والاستنتاجات بدقة، حيث تجدها في مجالات عدة مثل الرياضيات، المنطق، وغيرها من العلوم. تُساعد هذه الجمل في تكوين فهم واضح ومحدد للعلاقات بين أحداث معينة أو فرضيات. دعونا نستعرض خصائص الجمل الشرطية ببساطة:
– يتكون البناء الأساسي للجملة الشرطية من جزئين، الفرض ونتيجته، حيث يُعبَّر عن الفرض بطريقة مباشرة، وتسبق النتيجة عادةً بكلمة “إذن” أو ما يشابهها.
– هذه الجمل تتألف من جزأين مترابطين يُشكّلان معًا وحدة معنوية واحدة، يُعرض الجزء الأول منها الفكرة الأساسية أو الحدث المفترض، ويتبعه الجزء الثاني مباشرةً ليُظهر النتيجة أو التأثير الناجم عن الفرض.
– الهدف من الجمل الشرطية هو إيصال فكرة محددة وواضحة تتعلق بسياق معين، وترتبط الفكرتان المطروحتان في الجملة ببعضهما بشكل وثيق.
إن مفهوم الجمل الشرطية سهل ومباشر، وتستخدم بكثرة للتعبير عن العلاقات السببية والنتائج المتوقعة في ظروف محددة، مما يجعلها أداة قيّمة في اللغة وطريقة فعّالة للتواصل الواضح والمحدد.
جدول العبارات الشرطيه
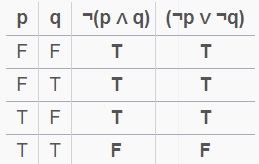
يشرح جدول الشروط كيفية تحديد صحة أو خطأ الجمل الشرطية بناءً على مختلف الحالات. الجمل الشرطية تعتمد على شرط معين لتحديد نتيجتها، وتعتبر خاطئة فقط عندما يكون الشرط محققًا بينما النتيجة غير صحيحة. في جميع الحالات الأخرى، تُعتبر الجملة صحيحة. الطريقة التي تعمل بها هذه القواعد مفصلة في الجدول التوضيحي.
جدول الصواب للعبارة الشرطيه
توجد علاقة بسيطة بين عبارتين، نسمي الأولى “ب” والثانية “ق”. تُظهر هذه العلاقة كيف يمكن أن تؤثر صحة أو عدم صحة عبارة على الأخرى. عندما تكون العبارة “ب” صحيحة، يترتب على ذلك صحة “ق” أيضًا. لكن، في حالات معينة، يمكن أن تكون “ق” صحيحة بغض النظر عن “ب”.
لنوضح ذلك بأمثلة:
1. إذا كانت “ب” صحيحة و”ق” صحيحة أيضًا، فهذا يطابق توقعاتنا بأن صحة “ب” تضمن صحة “ق”.
2. لكن، إذا كانت “ب” صحيحة و”ق” خاطئة، فهذا يتنافى مع توقعاتنا ويعتبر خطأ، لأن “ب” الصحيحة يجب أن تؤدي إلى صحة “ق”.
3. إذا كانت “ب” خاطئة بينما “ق” صحيحة، هذا الوضع مقبول لأن صحة “ق” لا تعتمد بالضرورة على “ب” في هذا السياق.
4. وأخيرًا، إذا كانت كل من “ب” و”ق” خاطئتين، فهذا الوضع مقبول أيضًا لأن عدم صحة “ب” لا تؤدي بالضرورة إلى عدم صحة “ق”.
من خلال هذه الأمثلة، نستكشف كيف تتأثر صحة عبارة بأخرى مرتبطة بها، ونفهم أن هناك حالات يمكن فيها لعبارة أن تكون صحيحة بصرف النظر عن صحة أو عدم صحة العبارة الأخرى.
جدول العبارات الشرطيه المرتبطة
| النوع | الوصف | الرمز | أمثلة |
| شرطية | تستند إلى شرط يؤدي لنتيجة معينة | p → q | إن كانت زاويتان بنفس القياس فهما متماثلتان |
| عكسية | تقليب الشرط والنتيجة محل بعضهما | q → p | إن كانت زاويتان متماثلتان فقياسهما متساو |
| معكوسة | نقيض الفرض والنتيجة معاً | ~p → ~q | إن لم تكن زاويتان بنفس القياس فهما ليستا متماثلتين |
| عكسية موجبة | نقيض الفرض والنتيجة في العكس | ~q → ~p | إن لم تكون الزاويتان متماثلتان فقياسهما ليس متساو |
خصائص العبارات الشرطيه
الجمل الشرطية تأتي بأشكال متعددة، سواء كانت مختصرة أو مفصلة، لكنها جميعاً تشترك في هيكل يبتدئ بفكرة مُفترضة يتبعها تأثير أو نتيجة معينة. هذه البنية تعد القلب النابض للجملة الشرطية. من هذه العلاقة بين الفرض والنتيجة، تنبثق عدة إمكانيات يمكن أن تكون صحيحة أو غير ذلك. فيما يخص خصائص هذا النوع من الجمل، فهي تكمن في النقاط التالية:
– الجمل الشرطية تندرج تحت طائفة الجمل المترابطة.
– تتميز بوجود علاقة بين الافتراض وما يترتب عليه من نتائج.
– لا تعمل هذه الجمل بمعزل عن غيرها.
– لكل جملة شرطية ترابطية يمكن العثور على الجملة المعكوسة لها.
– يمكن أيضاً إنشاء جملة معاكسة إيجابية من الجملة الأصلية.
– هذا النوع من الجمل يبقى مطابقاً منطقياً؛ أي يحافظ على نفس قيمة الصحة في جميع الظروف.
– الجمل المنطقياً متكافئة تشترك في الصواب بجميع الحالات.
– يمكن أن تتشكل الجملة الشرطية بشكل ثنائي.
– وتعني أنها تضم الجملة الأصلية ونقيضها، محافظة بذلك على بناء الفرضية والنتيجة.
ما هي العبارات الشرطية المرتبطة
تشكل العبارات المقابلة جزءاً من الجمل الشرطية. هذه العبارات تستعمل للتعبير عن فكرة معاكسة لما جاء في الجملة الأصلية، بطريقة تعكس صورة إيجابية أو سلبية. دعونا نستعرض مثالاً يوضح هذه الفكرة:
– لدينا مثال يبين كيفية استخدام العبارة المقابلة في الجمل الشرطية:
– إذا كان الرقم الأخير في العدد صفر، فهذا يعني أن العدد يمكن قسمته على عشرة.
في هذا السياق، من الممكن أن نقلب الجملة ونقدم النتيجة في مكان الشرط، مثلما في القول:
– يمكن أيضاً قول إن إذا استطعت قسمة العدد على عشرة، فإن آخر رقم فيه سيكون صفراً.
بالإضافة إلى ذلك، هناك طريقة أخرى تنطوي على نفي كل من الشرط والنتيجة. يمكن توضيح ذلك من خلال القول:
– إذا لم يكن الرقم الأخير في العدد صفراً، هذا يعني أن العدد لا يمكن قسمته بسهولة على عشرة.
من خلال هذا الشرح، نرى كيف يمكن للجمل المقابلة أو العكسية أن تساعد في فهم علاقة معينة بين أفكار مختلفة بطريقة أكثر وضوحاً.
ما هي العبارات الشرطية الثنائية
العبارات التي تتطلب شرطاً معيناً ليتحقق شيء ما، وفي الوقت نفسه، يطلب هذا الشيء لتحقيق الشرط، تعرف بأنها شرطية ثنائية الاتجاه. وتعبر عن فكرة أن حدوث أمر ما يتوقف على شرط محدد، وبالمثل، يمكن استنتاج الشرط من تحقق الأمر. فهذه العبارات توضح علاقة تبادلية بين شرط ونتيجة يعزز بعضها بعضاً. ومن الأمثلة على هذه العبارات نجد:
– تُعرف الزاوية بأنها قائمة إذا كان قياسها يساوي 90 درجة، وبالتالي، إذا كانت زاوية قائمة فهذا يعني أن قياسها 90 درجة.
– بالمثل، زاويتان تكونان متتامتين إذا كان مجموع قياسهما يعادل 90 درجة. وإذا كان مجموع قياس زاويتين 90 درجة، فهما بذلك زاويتان متتامتان.
أمثلة على العبارات الشرطية
تُعَدُّ الجمل الشرطية جزءًا لا يتجزأ من العديد من مجالات العلم والمعرفة، وتُستخدم في تشكيل أساس للوصول إلى نتائج محددة. في ميدان الرياضيات، تلعب هذه الجمل دورًا رئيسيًا، وهي أيضًا مهمة في اللغة العربية بالإضافة إلى استخدامها في الكثير من المجالات الأخرى. تتكون الجمل الشرطية من شقين رئيسيين: الشرط وما يترتب عليه، حيث يرتبط كل من الشرط والنتيجة ارتباطًا وثيقًا بالآخر. من بين الأمثلة المشهورة للجمل الشرطية نجد:
– إذا كان للمثلث زاوية قائمة، فهذا يعني أن له زاوية واحدة قائمة.
– إذا كان المثلث قائماً، يجب أن تكون زاويتاه الأخريان حادتين.
– إذا كنا في يوم تهطل فيه الأمطار، فإن حمل المظلة يصبح ضروريًا.
– الثدييات هي فئة من الكائنات ذات درجة حرارة دم ثابتة.
– إذا كان الكائن ثدييًا، فهو من الكائنات ذات درجة حرارة دم ثابتة.
– إذا كان المنشور يتألف من قاعدة ذات شكل مضلع منتظم، فإن المنشور نفسه يعتبر منتظمًا.
– إذا كان للشكل الهندسي أربع أضلاع، فإنه يُصبح مضلعًا مقعرًا.
– إذا كانت الدائرة تمتلك “أضلاعًا”، فهذه “الأضلاع” تكون متساوية الطول.
هذه الأمثلة تُظهر الدور الكبير للجمل الشرطية في توضيح وفهم العديد من المفاهيم والقوانين في مختلف المجالات.
خاتمة بحث عن العبارات الشرطية
لقد قدمنا شرحًا وافيًا عن العبارات الشرطية ومدى أهميتها، موضحين كيف تعد ركنًا مهمًا في مجال الرياضيات وكذلك في العديد من العلوم الأخرى. نجد أن هذه العبارات ليست فقط جزءًا لا يتجزأ من الدراسات الأكاديمية، بل هي أيضًا ضرورية لفهم وتفسير العديد من الجوانب في العلوم والحياة العملية.